La fracción que señala la flecha en la recta numérica: todo lo que necesitas saber

La recta numérica es una herramienta utilizada en matemáticas para representar los números de manera ordenada. Cada punto en la recta corresponde a un número real y se puede utilizar para ubicar fracciones. Sin embargo, cuando se trata de una fracción representada en la recta numérica con una flecha, puede haber cierta confusión sobre su significado. Exploraremos qué representa exactamente la fracción señalada por una flecha en la recta numérica y cómo podemos interpretarla.

Discutiremos el concepto de una fracción señalada por una flecha en la recta numérica. Explicaremos cómo interpretar y entender qué representa esa fracción en términos de posición y magnitud. También exploraremos algunas reglas básicas para ubicar fracciones en la recta numérica y cómo convertir entre fracciones y números decimales para una mejor comprensión. Con esta información, podrás entender y utilizar adecuadamente las fracciones señaladas por una flecha en la recta numérica en tus estudios de matemáticas.

Qué es una fracción y cómo se representa en una recta numérica

Una fracción es una forma de representar una cantidad que está comprendida entre dos números enteros. Se compone de dos elementos principales: el numerador y el denominador. El numerador indica la cantidad de partes que se toman de un total, mientras que el denominador indica en cuántas partes se ha dividido ese total.

En una recta numérica, las fracciones se representan mediante una flecha que señala el punto correspondiente en relación a los números enteros. La posición de la flecha indica el valor exacto de la fracción y nos permite entender su ubicación y relación con otros números en la recta.

Cómo interpretar una fracción en la recta numérica

Para interpretar una fracción en la recta numérica, es importante recordar que cuanto más cerca esté la flecha del cero (izquierda), la fracción será más pequeña. Por otro lado, cuanto más cerca esté la flecha del uno (derecha), la fracción será más grande.

Por ejemplo, si tenemos la fracción 1/2, la flecha estaría situada exactamente a mitad de camino entre el cero y el uno en la recta numérica. Esto indica que la fracción 1/2 representa la mitad del segmento total en la recta. Si tenemos la fracción 3/4, la flecha estaría situada más cerca del uno que del cero, pero no llegando a él completamente. Esto nos indica que la fracción 3/4 es mayor que la mitad pero menor que la unidad.

Es importante destacar que cada fracción tiene una ubicación precisa en la recta numérica, lo que ayuda a comprender su valor relativo y su posición en relación con otros números.

Uso de la recta numérica para comparar fracciones

La recta numérica es una herramienta útil para comparar fracciones. Si tenemos dos fracciones, podemos colocar ambas flechas correspondientes en la recta y comparar sus posiciones relativas.

Por ejemplo, si queremos comparar las fracciones 1/4 y 2/4, trazaríamos las respectivas flechas en la recta numérica y observaríamos que la flecha de la fracción 2/4 estaría ubicada más cerca del uno que la flecha de la fracción 1/4. Esto indica que 2/4 es mayor que 1/4.

De manera similar, si queremos comparar las fracciones 1/2 y 2/3, trazaríamos las flechas correspondientes y notaríamos que la flecha de la fracción 2/3 estaría ubicada más cerca del uno que la flecha de la fracción 1/2. Esto nos indica que 2/3 es mayor que 1/2.

Ejemplos de fracciones en la recta numérica

A continuación, presentaremos algunos ejemplos de fracciones y su representación en la recta numérica:

• La fracción 1/3 se representa en la recta numérica como una flecha ubicada a aproximadamente un tercio del camino entre el cero y el uno.
• La fracción 3/5 se representa como una flecha ubicada a aproximadamente tres quintos del camino entre el cero y el uno.
• La fracción 7/8 se representa como una flecha ubicada muy cerca del uno, pero sin llegar a él completamente. Esto indica que la fracción 7/8 es mayor que siete octavos del camino entre el cero y el uno.

Estos ejemplos ilustran cómo las fracciones se representan en la recta numérica y cómo podemos utilizar esta herramienta para comprender mejor su valor relativo y su posición en relación con otros números.

Cuál es el significado de la flecha que señala una fracción en una recta numérica

La flecha que señala una fracción en una recta numérica es un recurso visual muy utilizado en matemáticas para representar números racionales de forma gráfica. Esta flecha nos indica cuál es la ubicación exacta de la fracción en la recta y nos permite comprender mejor su posición con respecto a otros números.

Cuando trazamos una recta numérica, generalmente empezamos por colocar los números enteros principales (como el cero, el uno, el dos, etc.) a intervalos regulares. Luego, para representar una fracción en específico, utilizamos una flecha que parte desde el número entero anterior y apunta hacia el número correspondiente a la fracción en cuestión.

Por ejemplo, si queremos representar la fracción 1/2 en una recta numérica, comenzamos trazando la línea horizontal y ubicamos el número 0 a la izquierda. Luego trazamos una flecha desde el 0 hasta el 1, indicando que estamos en el punto medio entre ellos. En la punta de la flecha, escribimos la fracción 1/2 para dejar claro qué valor representa.

Es importante tener en cuenta que la longitud de la flecha que señala la fracción no tiene ningún significado matemático en sí mismo. La clave está en la posición de la flecha en relación con los otros números y cómo se encuentra ubicada en la recta numérica. La longitud de la flecha puede variar dependiendo del espacio disponible en la representación gráfica.

Al utilizar las flechas para señalar fracciones en una recta numérica, podemos comparar diferentes números racionales y observar su posición relativa en la recta. Por ejemplo, si comparamos las fracciones 1/4 y 3/4, podemos ver que la flecha que representa la fracción 3/4 estará más cerca del número 1 que la flecha que representa la fracción 1/4.

Esta representación gráfica es especialmente útil cuando se trabaja con operaciones matemáticas que involucran fracciones, ya que nos permite visualizar fácilmente qué fracción es mayor o menor que otra, así como realizar sumas, restas, multiplicaciones y divisiones de fracciones de manera más intuitiva.

La flecha que señala una fracción en una recta numérica nos ayuda a visualizar la ubicación exacta de la fracción en relación con otros números racionales. Nos brinda una herramienta gráfica para comprender mejor el valor de una fracción y compararlo con otras, facilitando así el estudio y la manipulación de las fracciones de forma visual y práctica.

Cómo interpretar la posición de la flecha en relación a otros números en la recta numérica

La recta numérica es una herramienta fundamental en matemáticas que nos permite visualizar y ubicar números de manera ordenada y secuencial. En ella, cada número se representa por un punto o una flecha que indica su posición relativa respecto a otros números.

¿Qué significa la flecha en la recta numérica?

La flecha en la recta numérica tiene un significado muy importante, ya que nos indica la dirección y el sentido de los números. Cuando la flecha apunta hacia la derecha, significa que los números están aumentando en valor a medida que nos movemos hacia ese lado. Por otro lado, cuando la flecha apunta hacia la izquierda, implica que los números están disminuyendo en valor a medida que nos alejamos en esa dirección.

Es importante tener en cuenta que los números pueden ser enteros, decimales o fracciones, y su posición en la recta numérica estará determinada por su valor numérico. Además, la distancia entre dos puntos consecutivos en la recta numérica es siempre la misma, lo que nos permite tener una referencia constante para comparar los valores de diferentes números.

Utilizando la fracción para indicar la posición de la flecha

En algunos casos, puede que la flecha en la recta numérica venga acompañada de una fracción. Esta fracción nos proporciona información adicional sobre la posición exacta del número representado por la flecha.

Por ejemplo, si tenemos una flecha que apunta hacia la derecha y viene acompañada de la fracción 1/4, esto significa que el número representado se encuentra en una posición entre dos números enteros consecutivos, y su valor es una cuarta parte del intervalo entre estos dos números. Siguiendo este ejemplo, si la flecha está ubicada después del número 2 en la recta numérica, el número representado sería 2 + 1/4 = 2.25.

De manera similar, si la flecha apunta hacia la izquierda y viene acompañada de una fracción, esto indica que el número representado se encuentra antes del número entero más cercano y su valor también está determinado por la fracción asociada. Por ejemplo, si la flecha está ubicada antes del número 0 y lleva la fracción -3/5, el número representado sería -3/5.

La posición de la flecha en la recta numérica es crucial para interpretar y comparar diferentes números. A través de la dirección y sentido de la flecha, así como de las fracciones asociadas, podemos entender con mayor precisión la ubicación de un número en relación a otros números en la recta numérica. Esta herramienta nos ayuda a desarrollar habilidades matemáticas fundamentales y nos permite realizar operaciones más complejas como la suma, resta, multiplicación y división de números enteros, decimales y fracciones.

Qué información nos proporciona la fracción y la flecha en términos de magnitud

La fracción que señala la flecha en la recta numérica es una representación visual de un número en forma de fracción, la cual indica su magnitud o posición en relación con otros números en la recta.

La fracción en sí misma nos proporciona dos piezas clave de información: el numerador y el denominador. El numerador representa la cantidad de partes que estamos considerando, mientras que el denominador indica el número total de partes en la unidad.

Por ejemplo, si tenemos la fracción 3/4 representada en la recta numérica, esto significa que estamos considerando tres partes de un todo dividido en cuatro partes iguales. La flecha, por otro lado, nos indica cuál es el punto específico en la recta que corresponde a esa fracción. Es decir, la flecha apunta a la posición exacta que representa el número 3/4 en la recta numérica.

Es importante tener en cuenta que la fracción y la flecha juntas nos brindan información sobre la magnitud del número representado. En este caso, la fracción 3/4 indica que el número está más cerca del valor máximo posible (1) que del valor mínimo posible (0) en la recta numérica.

Al examinar otras fracciones en la recta numérica, podemos observar cómo cambia su magnitud y su posición en relación con otros números. Por ejemplo, si tenemos la fracción 1/2, estará ubicada en el punto medio entre los valores mínimos y máximos posibles, lo cual indica que su magnitud es menor que 3/4 pero mayor que 1/4.

Para comprender completamente la magnitud de una fracción representada en la recta numérica, también podemos utilizar otras herramientas, como un gráfico o una tabla de valores. Estas representaciones adicionales nos ayudan a visualizar y comparar las magnitudes de diferentes fracciones.

Cómo utilizar la información de la fracción y la flecha

La información proporcionada por la fracción y la flecha en la recta numérica es útil en diversas situaciones matemáticas. Por ejemplo, al sumar o restar fracciones, podemos utilizar la ubicación de la flecha para determinar si los números que estamos combinando se acercan más al valor máximo o mínimo posible.

También podemos utilizar esta representación para ordenar fracciones de menor a mayor o de mayor a menor. Al observar la posición de las flechas en la recta numérica, podemos determinar fácilmente cuál fracción es mayor o menor que otra.

Además, la fracción y la flecha nos brindan una forma visual de entender la relación entre las partes y el todo en un contexto específico. A medida que exploramos más fracciones y sus ubicaciones en la recta numérica, podemos desarrollar una comprensión más profunda de cómo se relacionan con otros números y cómo varía su magnitud.

• Ejemplo 1: Si tenemos las fracciones 1/4, 2/4 y 3/4 en la recta numérica, podemos ver claramente cómo cada fracción se ubica en relación con las demás. La flecha de 1/4 estará más cerca del valor mínimo (0), mientras que la flecha de 3/4 estará más cerca del valor máximo (1), indicando que 3/4 es mayor que 1/4.
• Ejemplo 2: Si queremos determinar qué fracción es mayor entre 2/8 y 5/8, podemos examinar la ubicación de sus flechas en la recta numérica. Al estar ambas flechas en el mismo numerador (8), nos fijamos en el valor del denominador para comparar. En este caso, 5/8 está más cerca del valor máximo (1) que 2/8, lo que indica que 5/8 es mayor que 2/8.

Cuáles son los diferentes tipos de fracciones que podemos encontrar en una recta numérica

La recta numérica es una herramienta fundamental en la matemática, especialmente cuando se trata de trabajar con fracciones. Una fracción señala la posición entre dos números enteros en la recta numérica. Pero, ¿sabías que existen diferentes tipos de fracciones que podemos encontrar en esta representación visual?

En primer lugar, tenemos las fracciones propias. Estas son aquellas en las que el numerador es menor que el denominador. Por ejemplo, si tenemos la fracción 1/2, podemos ubicarla en la recta numérica entre los números 0 y 1. Es importante destacar que la fracción 1/2 representa la mitad del intervalo entre estos dos números.

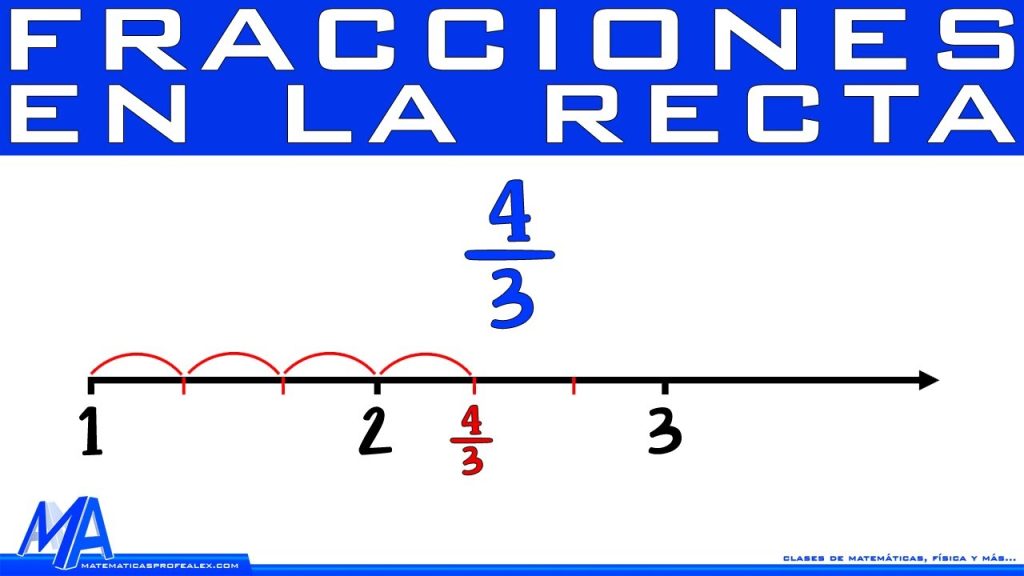
Por otro lado, encontramos las fracciones impropias. Estas son aquellas en las que el numerador es igual o mayor que el denominador. Si tenemos la fracción 5/3, por ejemplo, podemos ubicarla en la recta numérica entre los números 1 y 2. En este caso, la fracción 5/3 representa un valor mayor a 1 unidad.

Otro tipo de fracción que podemos encontrarnos en la recta numérica son las fracciones mixtas. Estas son combinaciones de números enteros y fracciones propias. Por ejemplo, si tenemos la fracción mixta 2 1/4, podemos ubicarla en la recta numérica entre los números 2 y 3. La parte entera, en este caso el número 2, se coloca primero y luego se coloca la fracción propia 1/4.

¿Cómo podemos representar estas fracciones en la recta numérica?

Para representar una fracción en la recta numérica, es importante recordar que el numerador señala la cantidad de intervalos que debemos avanzar desde el número inicial y el denominador señala la cantidad total de intervalos entre ambos números.

Por ejemplo, si queremos representar la fracción 2/3 en la recta numérica entre los números 0 y 1, primero dividimos el intervalo entre estos dos números en tres partes iguales. Luego, a partir del número 0, avanzamos dos de estas tres partes para marcar la ubicación de la fracción 2/3.

Es importante mencionar que el punto o flecha que marca la posición de la fracción en la recta numérica se coloca justo en el límite del intervalo. En el caso de la fracción 2/3, la flecha se colocaría exactamente 2/3 del camino desde el número 0 al número 1.

Ejemplo:

Supongamos que queremos representar la fracción 3/4 en la recta numérica entre los números 0 y 1. Dividimos el intervalo en cuatro partes iguales y avanzamos tres de estas partes desde el número 0. La flecha se colocaría justo en el límite entre la tercera y cuarta parte del intervalo.

Las fracciones pueden ser representadas en la recta numérica de diferentes formas dependiendo de si son propias, impropias o mixtas. Además, es importante recordar que el numerador indica la cantidad de intervalos que debemos avanzar y el denominador señala la cantidad total de intervalos entre ambos números.

Ahora que conoces los diferentes tipos de fracciones y cómo representarlos en la recta numérica, podrás utilizar esta herramienta de forma efectiva para entender mejor las relaciones entre los números.

Cómo podemos utilizar la fracción y la flecha para ordenar números en una recta numérica

La recta numérica es una herramienta fundamental en matemáticas para representar y ordenar números. Nos permite visualizar de forma clara la relación y el orden entre los números. Pero, ¿qué ocurre cuando queremos representar fracciones en una recta numérica?

En este artículo hablaremos sobre la fracción que señala la flecha en la recta numérica y cómo podemos utilizarla para ordenar números. La fracción alude a una parte de un todo, y su representación en la recta numérica nos ayuda a comprender mejor la ubicación y el valor relativo de distintos números.

Representando fracciones en la recta numérica

Para representar una fracción en la recta numérica, primero debemos dividir la distancia total en partes iguales, donde cada parte representa una unidad. Luego, colocaremos la fracción correspondiente en la posición adecuada de la recta. Por ejemplo, si tenemos la fracción 1/2, dividiremos la recta numérica en dos partes iguales y marcaremos la mitad.

Es importante recordar que la fracción se coloca siempre a la derecha de la marca en la recta numérica. Esto se debe a que la flecha indica hacia dónde se va a contar, y al estar a la derecha de la fracción, estamos contando hacia adelante.

Ordenando números con la fracción y la flecha

Una vez que hemos representado las fracciones en la recta numérica, podemos utilizarlas para ordenar números. Para ello, podemos seguir estos pasos:

1. Identificar las fracciones en la recta numérica y determinar su valor relativo. Por ejemplo, si tenemos las fracciones 1/3, 2/6 y 4/8, debemos observar que todas representan la misma cantidad, ya que todas se encuentran en el mismo punto de la recta.
2. Comparar los números que están a la izquierda y a la derecha de cada fracción en la recta numérica. Esto nos permite establecer relaciones de orden entre los números. En el ejemplo anterior, podemos observar que 1/3 está a la izquierda de 2/6 y 4/8, lo que nos indica que 1/3 es menor que 2/6 y 4/8.
3. Repetir el proceso con todas las fracciones presentes en la recta numérica hasta establecer un orden completo.

Cabe destacar que este método también puede ser utilizado para ordenar números mixtos o enteros en una recta numérica. Si tenemos números mixtos, debemos convertirlos a fracciones antes de representarlos y compararlos en la recta.

Ejemplo práctico

Para entender mejor cómo utilizar la fracción que señala la flecha en la recta numérica, veamos un ejemplo:

Supongamos que queremos ordenar los siguientes números en una recta numérica: 1/2, 3/4, y 5/8. Siguiendo los pasos descritos anteriormente, dividiremos la recta numérica en partes iguales, colocaremos las fracciones correspondientes en su posición correcta y compararemos los números adyacentes.

1. Primero, dividiremos la recta numérica en 8 partes iguales y marcaremos cada fracción:


0/8 1/8 2/8 3/8 4/8 5/8 6/8 7/8 8/8


2. Ahora, compararemos las fracciones adyacentes para ordenar los números:


0/8 1/8 2/8 3/8 4/8 5/8 6/8 7/8 8/8

^ ^ ^
| | |

1/2 3/4 5/8


En este ejemplo, podemos observar que 1/2 está a la derecha de 3/4 y 5/8, lo que nos indica que 1/2 es mayor que 3/4 y 5/8. Por lo tanto, el orden correcto de los números en la recta numérica sería: 5/8, 3/4 y 1/2.

Como podemos ver, utilizar la fracción que señala la flecha en la recta numérica es una estrategia efectiva para ordenar números de manera visual y comprender su relación y valor relativo. Esta técnica puede ser utilizada no solo en ejercicios teóricos, sino también en problemas prácticos de la vida cotidiana donde se requiera ordenar números o realizar comparaciones.

La fracción que señala la flecha en la recta numérica es una herramienta valiosa que nos permite ordenar números de forma visual y comprender su relación. Dividir la recta en partes iguales y colocar las fracciones correspondientes nos ayuda a establecer un orden claro y entender el valor relativo entre los números. Esto resulta especialmente útil tanto en ejercicios teóricos como en situaciones prácticas de la vida cotidiana.

Cuál es la relación entre las fracciones, las flechas y los intervalos en una recta numérica

Las fracciones son una parte fundamental de las matemáticas y se utilizan para representar partes de un todo. En la recta numérica, las fracciones se pueden ubicar en puntos específicos utilizando flechas y intervalos. En este artículo, te explicaré en detalle la relación entre las fracciones, las flechas y los intervalos en una recta numérica.

¿Qué es una recta numérica?

Antes de profundizar en la relación entre las fracciones, las flechas y los intervalos, es importante comprender qué es una recta numérica. Una recta numérica es una línea recta en la que se representan los números reales. Permite visualizar y ordenar los números de manera secuencial, desde el menor al mayor.

Las fracciones en la recta numérica

Para representar una fracción en una recta numérica, se utiliza una flecha que señala un punto específico sobre la línea. Esta flecha indica el valor de la fracción y su posición con respecto a otros números en la recta. A medida que nos acercamos al lado derecho de la recta, los valores de las fracciones aumentan, mientras que al acercarnos al lado izquierdo disminuyen.

Por ejemplo, si queremos representar la fracción 1/2 en una recta numérica, dibujaremos una flecha que parte del origen y apunta hacia la mitad del segmento entre el 0 y el 1. Esto indica que la fracción 1/2 se encuentra justo en el medio de la escala numérica.

Los intervalos en la recta numérica

Los intervalos son segmentos de la recta numérica que se utilizan para agrupar conjuntos de números. Estos intervalos pueden ser abiertos, cerrados o semiabiertos, dependiendo de si los extremos del intervalo están incluidos o excluidos.

Cuando representamos una fracción en una recta numérica, generalmente se utiliza un intervalo cerrado, es decir, ambos extremos del segmento están incluidos. Esto se debe a que las fracciones representan partes exactas de un todo y, por lo tanto, no permiten ningún número adicional entre los valores indicados por la flecha.

La relación entre las fracciones, las flechas y los intervalos

Las fracciones se representan en una recta numérica utilizando flechas que indican su valor y posición específica. Estas flechas se ubican en intervalos cerrados, que agrupan los conjuntos de números que representan las fracciones.

Es importante comprender esta relación para poder trabajar con fracciones en la recta numérica de manera correcta. La ubicación de las flechas y la elección de los intervalos adecuados nos permite comparar, ordenar y operar con fracciones de manera precisa.

Ahora que conoces la relación entre las fracciones, las flechas y los intervalos en una recta numérica, podrás utilizar esta herramienta para representar y entender mejor las fracciones. ¡Exploremos juntos el fascinante mundo de las matemáticas!

Cuáles son algunos ejemplos prácticos de situaciones donde el uso de fracciones y la flecha en una recta numérica es útil

Las fracciones y la representación gráfica en una recta numérica son herramientas fundamentales en el estudio de las matemáticas y tienen aplicaciones prácticas en diversas situaciones de la vida cotidiana. A continuación, te presentamos algunos ejemplos donde el uso de fracciones y la flecha en una recta numérica es muy útil:

1. Medidas en la cocina

En la cocina, las recetas suelen requerir medidas precisas de los ingredientes. En muchas ocasiones, estas medidas no se cuentan con números enteros, sino que se utilizan fracciones. La recta numérica puede ser una gran ayuda para visualizar las diferentes medidas y hacer conversiones entre fracciones. Por ejemplo, si necesitas agregar 1/4 de taza de azúcar a una receta, puedes ubicar 1/4 en la recta numérica y luego contar los espacios hasta llegar al número deseado.

2. Porcentajes y proporciones

En el ámbito financiero y comercial, los porcentajes y las proporciones son conceptos constantemente utilizados. La representación gráfica de fracciones en la recta numérica permite entender de forma visual cómo se distribuyen las proporciones y cómo se relacionan con los porcentajes. Por ejemplo, si quieres calcular un descuento del 20% en un producto, puedes utilizar la recta numérica para visualizar fácilmente cuánto sería ese descuento en términos de fracción.

3. Tiempo y duración

El tiempo y la duración son magnitudes que también se pueden expresar mediante fracciones. Para representar eventos que duran una fracción de hora o fracciones de minutos, la recta numérica puede ser utilizada para entender visualmente cuánto tiempo ha transcurrido o cuánto tiempo queda. Por ejemplo, si tienes un evento de 1/3 de hora de duración, puedes ubicarlo en la recta numérica y observar fácilmente cuánto tiempo queda hasta su finalización.

4. Compartir y repartir

En situaciones cotidianas donde es necesario compartir o repartir algo entre varias personas, las fracciones y la recta numérica ayudan a visualizar de manera precisa cómo se divide o distribuye esa cantidad. Por ejemplo, si tienes una pizza y quieres repartirla en partes iguales entre 4 personas, puedes utilizar la recta numérica para marcar el punto de inicio y final de cada porción igual.

5. Proporción de mezclas

En diversas actividades como la cocina, la química o la industria, es común necesitar hacer mezclas de diferentes componentes o sustancias en proporciones específicas. La recta numérica puede ser utilizada para visualizar claramente cuánto de cada componente se necesita y cómo se deben combinar en la mezcla final. Por ejemplo, si debes preparar una solución de agua y azúcar en una proporción de 2:3, puedes utilizar la recta numérica para determinar las cantidades exactas de cada elemento.

Estos son solo algunos ejemplos prácticos donde el uso de fracciones y la flecha en una recta numérica resultan extremadamente útiles. A través de su representación gráfica, podemos entender mejor las relaciones numéricas y resolver problemas de manera más eficiente. ¡Explora estas aplicaciones en tu día a día y descubre cómo las matemáticas están presentes en todo lo que nos rodea!

Cómo podemos resolver problemas matemáticos utilizando la fracción y la flecha en una recta numérica

La fracción es una herramienta fundamental en matemáticas que nos permite representar partes de un todo. Cuando combinamos la fracción con la recta numérica, podemos visualizar y resolver problemas matemáticos de una manera más clara y práctica.

La primera pregunta que nos podemos hacer es ¿cómo se representa una fracción en la recta numérica? La respuesta es sencilla: utilizando una flecha. Cada fracción tiene un numerador (el número de arriba) y un denominador (el número de abajo). El numerador indica cuántas partes del todo vamos a considerar y el denominador indica en cuántas partes ha sido dividido el todo.

Por ejemplo, si tenemos la fracción 2/5, debemos dibujar una flecha que empiece en cero (el punto de referencia en la recta numérica) y que se extienda hasta la quinta parte de la recta. Luego, debemos marcar dos quintas partes desde el punto de partida. De esta manera, hemos representado correctamente la fracción 2/5 en la recta numérica.

Pero, ¿cómo podemos utilizar esta representación para resolver problemas matemáticos? La respuesta está en el análisis de las posiciones de las flechas en la recta numérica.

Suma y resta de fracciones utilizando la recta numérica

Una de las operaciones más comunes que realizamos con fracciones es la suma y resta. Utilizando la recta numérica, podemos visualizar estas operaciones de una manera intuitiva.

Supongamos que tenemos las fracciones 1/4 y 1/3. Si representamos estas fracciones en la recta numérica, podemos observar que la flecha correspondiente a 1/3 es más larga que la flecha correspondiente a 1/4. Esto significa que 1/3 representa una cantidad mayor que 1/4.

Para realizar la suma de estas fracciones, debemos encontrar un punto en la recta numérica que esté a la misma distancia tanto de 1/4 como de 1/3. En otras palabras, debemos buscar un punto que se encuentre justo a la mitad entre los dos extremos de las flechas.

Utilizando la recta numérica, podemos ver que este punto corresponde a la fracción 7/12. Por lo tanto, la respuesta a la suma de 1/4 y 1/3 es 7/12.

De manera similar, para realizar la resta de fracciones utilizando la recta numérica, debemos buscar un punto que esté justo a la mitad entre los dos extremos de las flechas correspondientes a las fracciones que queremos restar. Este punto nos indicará el resultado de la resta.

Multiplicación y división de fracciones utilizando la recta numérica

Otra operación importante con fracciones es la multiplicación y la división. Al igual que con la suma y la resta, la recta numérica puede ayudarnos a visualizar y resolver estos problemas de manera más sencilla.

Para la multiplicación de fracciones, podemos usar la recta numérica para representar cada una de las fracciones y luego buscar el punto donde se cruzan las flechas. Este punto indicará el resultado de la multiplicación.

Por ejemplo, si tenemos las fracciones 2/3 y 1/5, podemos representar ambas en la recta numérica y encontrar el punto de intersección. En este caso, el punto de intersección corresponde a la fracción 2/15. Por lo tanto, el resultado de la multiplicación es 2/15.

En cuanto a la división de fracciones, podemos utilizar la recta numérica para visualizar cómo una fracción se divide por otra. En lugar de dibujar una flecha que va desde cero hasta el denominador, dibujaremos dos flechas: una que representa la fracción dividendo y otra que representa la fracción divisor. El punto donde se cruzan estas flechas nos indica el resultado de la división.

Por ejemplo, si queremos dividir 3/4 entre 2/5, debemos representar ambas fracciones en la recta numérica y encontrar el punto de intersección de las flechas correspondientes. En este caso, el punto de intersección corresponde a 15/8. Por lo tanto, el resultado de la división es 15/8.

Utilizar la fracción y la flecha en la recta numérica es una forma efectiva de resolver problemas matemáticos relacionados con sumas, restas, multiplicaciones y divisiones. Esta representación nos permite visualizar de manera clara las relaciones entre las fracciones y obtener resultados precisos. ¡No dudes en utilizar esta herramienta en tus ejercicios matemáticos!

¿Existen herramientas o recursos disponibles que nos ayuden a comprender y visualizar mejor las fracciones y la flecha en una recta numérica?

¡Por supuesto que sí! En la actualidad, existen diversas herramientas y recursos que nos permiten comprender y visualizar de manera más clara las fracciones y su representación en una recta numérica. Estas herramientas son especialmente útiles para estudiantes y personas que desean afianzar sus conocimientos matemáticos en este tema.

A continuación, te presentaré algunas de estas herramientas y recursos:

• 1. Aplicaciones móviles: Es posible encontrar en el mercado diferentes aplicaciones móviles diseñadas específicamente para ayudar a comprender las fracciones y su ubicación en una recta numérica. Estas aplicaciones suelen incluir actividades interactivas, ejercicios prácticos y explicaciones detalladas para facilitar el aprendizaje y la comprensión del tema.
• 2. Software educativo: Al igual que las aplicaciones móviles, existe software educativo disponible en línea que permite una mejor comprensión de las fracciones y la representación en la recta numérica. Estos programas suelen ofrecer una amplia variedad de actividades y ejercicios, adaptados a diferentes niveles de dificultad, lo que ayuda a los estudiantes a practicar y fortalecer sus habilidades matemáticas en este campo.
• 3. Pizarras interactivas: Las pizarras interactivas también son una excelente herramienta para enseñar y comprender las fracciones y la representación en la recta numérica. Estas permiten al profesor o facilitador mostrar gráficamente cómo se representa una fracción en la recta numérica y hacer demostraciones en tiempo real. Asimismo, los estudiantes pueden participar activamente en la construcción y manipulación de diferentes fracciones, lo que facilita su comprensión del concepto.
• 4. Videos educativos: En plataformas en línea como YouTube, se pueden encontrar numerosos videos educativos que explican de manera clara y concisa las fracciones y su ubicación en la recta numérica. Estos videos suelen utilizar animaciones y ejemplos visuales para ilustrar el concepto, lo que ayuda a los espectadores a comprender mejor cómo funciona este sistema de representación.

Existen diversas herramientas y recursos disponibles que nos ayudan a comprender y visualizar mejor las fracciones y la representación en una recta numérica. Ya sea a través de aplicaciones móviles, software educativo, pizarras interactivas o videos educativos, estos recursos brindan una oportunidad invaluable para fortalecer nuestras habilidades matemáticas y mejorar nuestra comprensión de este tema. ¡No dudes en aprovecharlos!

Qué consejos o recomendaciones puedes darme para mejorar mi comprensión y habilidades con respecto a las fracciones y la flecha en una recta numérica

Las fracciones son una parte fundamental de las matemáticas y pueden resultar confusas para algunas personas. Sin embargo, comprender el funcionamiento de una fracción y cómo se representa en una recta numérica puede mejorar significativamente tu comprensión y habilidades matemáticas.

Para mejorar tu comprensión y habilidades con respecto a las fracciones y la flecha en una recta numérica, aquí tienes algunos consejos y recomendaciones:

1. Familiarízate con los conceptos básicos de las fracciones

Antes de adentrarte en la representación de las fracciones en una recta numérica, es importante que entiendas los conceptos básicos de las fracciones. Asegúrate de comprender qué es una fracción, cómo se divide una cantidad en partes iguales y cómo se representa la fracción en forma de cociente.

2. Practica la conversión entre fracciones y números decimales

La conversión entre fracciones y números decimales es una habilidad clave cuando se trata de trabajar con fracciones en una recta numérica. Practica la conversión de fracciones a números decimales y viceversa utilizando diferentes métodos, como dividir o multiplicar por potencias de 10. Esto te ayudará a visualizar mejor la posición de una fracción en una recta numérica.

3. Utiliza recursos visuales

El uso de recursos visuales, como gráficos y diagramas, puede ser de gran ayuda cuando intentas comprender y representar fracciones en una recta numérica. Utiliza material didáctico, como rectas numéricas y modelos gráficos de fracciones, para visualizar mejor las relaciones entre diferentes fracciones y su posición en una recta numérica.

4. Practica con ejercicios y problemas

La práctica es fundamental cuando se trata de mejorar la comprensión y habilidades con respecto a las fracciones y la flecha en una recta numérica. Realiza ejercicios y problemas que implican trabajar con fracciones en una recta numérica. Esto te ayudará a familiarizarte con los conceptos y a desarrollar tus habilidades matemáticas.

5. Explora aplicaciones prácticas de las fracciones

Para contextualizar el aprendizaje de las fracciones en una recta numérica, explora aplicaciones prácticas de las fracciones en la vida cotidiana. Por ejemplo, cuando cocines una receta o al dividir una pizza entre amigos, observa cómo se pueden representar estas situaciones utilizando fracciones y una recta numérica. Esto te ayudará a comprender mejor la utilidad de las fracciones y su representación visual en una recta numérica.

Mejorar tu comprensión y habilidades con respecto a las fracciones y la flecha en una recta numérica requiere práctica, visualización, familiarización con los conceptos básicos y exploración de aplicaciones prácticas. Sigue estos consejos y recomendaciones, y estarás en el camino hacia un mejor dominio de las fracciones y su representación en una recta numérica.

Una fracción se representa en la recta numérica ubicando su punto medio entre los números enteros que la rodean.

El numerador es el número que está arriba de la línea fraccionaria y representa las partes que se toman, mientras que el denominador es el número que está abajo de la línea fraccionaria y representa las partes en las que se divide el total.

Para comparar una fracción con otra en la recta numérica, se observa cuál de las dos se encuentra más a la derecha. La que se encuentra más a la derecha es mayor.

Una fracción está en su forma más simple cuando el numerador y el denominador no tienen factores comunes excepto 1.

Si el denominador de una fracción es cero, la fracción se considera indefinida y no tiene valor numérico.